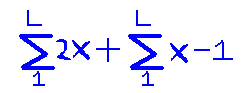
Purpose: Scientific AmeriKen strays away from typical science experiments this week to present a mathematical formula for determining the number of cards required to build a certain level sized card house. The formula, if proven true, can be a powerful ally in those seeking to break the card house height record.

Hypothesis: The formula is based on the assumption that the card house is a typical "A" framed card house. Given this, it is hypothesized that the formula will yield total number of cards required to build a certain story cardhouse.

Equipment: This experiment will require a pen and paper, calculator is optional, and cards are optional as card houses can be diagrammed.

Procedure: To prove the formula, one must run a number through, and build either a card house or diagram a cardhouse. Then compare the theoretical number of the formula with the actual number it took to produce the card house. For this experiment, the numbers 1, 2, 3, 5, and 10 were chosen. Each number will be processed as below...

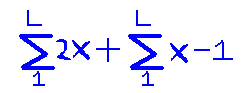
5 levels = (2x1)+(2x2)+(2x3)+(2x4)+(2x5)+(1-1)+(2-1)+(3-1)+

(4-1)+(5-1)=2+4+6+8+10+1+2+3+4

= 40 cards needed...

Observations:

Number of Levels	Formula Prediction	Actual Number	Cardhouse
1	2	2
2	7	7
3	15	15
5	40	40
10	110	110

Conclusion: Given the data, the hypothesis is confirmed, and the Seldeen Cardhouse formula accurately predicts the number of cards that are needed to form a theoretical model "A" frame cardhouse.

Back to the Scientific AmeriKen Homepage...