Purpose:  This week, Scientific AmeriKen will investigate the relationship between the distance an object is thrown and the weight of the object. An investigation sure to have powerful real world applications.

Hypothesis:  It is the hypothesis of this experiment is a linear relationship exist between throwing distance and the weight of an object. This implies that distance will have an inverse relationship with weight such that an increase in weight will decrease distance and vice-versa. This also implies that theoretical maximum distances and weights can be found for the thrower.

Equipment:  Needed for this experiment was a scale, rocks of various sizes, a pen and paper.

Procedure:  The first step is to measure and record the weight of the rocks, then throw the rocks in a consistent manner. Rocks thrown in this experiment were done so in a "two handed shot put" style.  Pace off or measure with a measuring tape the distance the rock travels. For each rock, repeat twice for right handed throws and twice for left handed throws. Average out the total from each trial, and plot weight vs  ave. distance traveled. Also, for each trial multiply distance traveled by the weight and compare for all trials.

Results:

Right Handed Results

Weight (lbs.)	Trial #1 Distance (ft.)	Trial #2 Distance (ft.)	Ave Distance (ft.)	Distance x Weight (ft. x  lbs)
9.5 Pounds Right Hand	37 Feet	37 Feet	37 Feet	351.5 ft-lbs
12.5 Pounds Right Hand	28 Feet	27 Feet	27.5 Feet	343.8 ft-lbs
27 Pounds Right Hand	19.5 Feet	21.5 Feet	20.5 Feet	553.5 ft-lbs
32 Pounds Right Hand	17 Feet	17.5 Feet	17.25 Feet	552.0 ft-lbs

Left Handed Results

Weight (lbs.)	Trial #1 Distance (ft.)	Trial #2 Distance (ft.)	Ave Distance (ft.)	Distance x Weight (ft. x  lbs)
9.5 Pounds Left Hand	29 Feet	27 Feet	28 Feet	266.0 ft-lbs
12.5 Pounds Left Hand	26 Feet	25 Feet	25.5 Feet	318.8 ft-lbs
27 Pounds Left Hand	18 Feet	19 Feet	18.5 Feet	499.5 ft-lbs
32 Pounds Left Hand	14.5 Feet	14 Feet	14.25 Feet	456.0 ft-lbs

 

Graph 1: Illustrates amount of force applied as a function of the weight of the rock.  R.H.= Right handed throws L.H.= Left handed throws

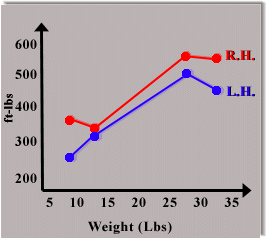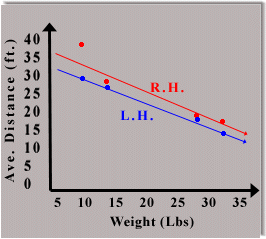Graph 2: Illustrates Distance rocks traveled as a function of their weight.  Eq of R.H. Throws R.H. : Y= -.698X + 39.1 Yint=39.1 (Theoretical Max Dis. any rock can be thrown in feet) Xint=56.1 (Theoretical heaviest Rock that can be tossed in lbs) Eq of L.H. Throws L.H. : Y= -.645X + 34.5 Yint=34.5 (Theo. Max Dis) Xint=53.5 (Theo. Max Weight) For how this information was found click here

Conclusion:  The results of this experiment yield some interesting information. Limited data allow for only a subjective view of the hypothesis's correctness. Judging from graph #2 it would seem as though linear best fit lines work nicely for L.H. results and moderatly well for R.H. results. This implies that the relationship between weight and throwing distance is linear. However, if this is the case, it would imply that a rock of greater weight then 56.1 lbs could not be thrown using the "shot putt" style, a fact that will remain untested until a rock of such size is found. Another interesting result which does not support the hypothesis is the large difference in amount of ft-lbs in the different throws. It is noted how the amount of force applied by the thrower increases as the weight of the object increases. Most likely one would expect that if distance had a linear relationship with object weight, then one would expect that inputed force would remain constant for all throws so that the only two variables remain distance or weight. For the sake of argument, Scientific AmeriKen accepts this second explanation, thus refuting the hypothesis, as we hope that we should be able to throw a wussy little 60 pound rock.